Tulos: Junior
Vastasit kysymykseen. Sinulta kysyttiin 15.
Alkupisteesi olivat 44. Jos vastasit kaikkiin tehtäviin väärin loppupisteesi olisivat 0.
Vastasit oikein 0 kysymykseen.
Vastasit väärin 0 kysymykseen.
Jätit vastaamatta 15 kysymykseen.
Pisteesi: 44/176
Hienoa!
Sait 0 pistettä tehtävästä "Metsän uutiset ".
Sait 0 pistettä tehtävästä "Majavaraiteet".
Sait 0 pistettä tehtävästä "Tulitikut".
Sait 0 pistettä tehtävästä "Majavakaupungin kadut".
Sait 0 pistettä tehtävästä "Eulerin polku".
Sait 0 pistettä tehtävästä "Listan muunnoksia".
Sait 0 pistettä tehtävästä "Loogiset toiminnot - kirjain E".
Sait 0 pistettä tehtävästä "Laula laulu".
Sait 0 pistettä tehtävästä "Sateenkaaren värit".
Sait 0 pistettä tehtävästä "Katkennut oksa".
Sait 0 pistettä tehtävästä "Tasapainotila".
Sait 0 pistettä tehtävästä "Karel kävelee kuutiolla".
Sait 0 pistettä tehtävästä "Sekoitettu väri".
Sait 0 pistettä tehtävästä "Menninkäiset".
Sait 0 pistettä tehtävästä "Sukupuu".
1. Metsän uutiset
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 6. Tehtävä oli tasoltaan helppo.
Majava-toimittaja julkaisee Metsän Uutiset -lehteä joenvarressa asettamalla pieniä kiviä ja tikkuja riviin kuvan tapaan. Muut majavat voivat lukea Metsän Uutiset ohi uidessaan. Jokainen sana Metsän Uutisissa on viisi tai kuusi kiveä tai tikkua pitkä.
Kuinka monta erilaista sanaa on mahdollista muodostaa Metsän Uutisissa?

| 1. |
96 |
Oikea vastaus |
| 2. |
64 |
|
| 3. |
720 |
|
| 4. |
2048 |
Et vastannut tähän kysymykseen.
Selitys:
Tehtävässä piti laskea Metsän Uutisten sanojen permutaatio. Permutaatiolla tarkoitetaan tässä yhteydessä sitä, monellako eri tavalla voidaan järjestää viiden tai kuuden merkin sarjoja kivestä ja kepistä. Koska mahdollisia sanojen pituuksia on kaksi, on kaikkien mahdollisten sanojen määrä mahdollisten viisi- ja kuusilukuisten sanojen määrien summa.
Viiden merkin erilaisten järjetyksien määrä lasketaan laskusta 25 = 32. Kakkonen tulee erilaisista merkeistä, joita ovat kivi ja keppi ja 5 tulee siitä, montako kyseisiä merkkejä voi yhdessä sanassa olla. Vastaavasti lasketaan kuuden merkin sarja, eli 26 = 64. Lopuksi nämä lasketaan yhteen ja saadaan 25 + 26 = 96.
Matematiikka kuuluu suurena osana tietojenkäsittelytieteeseen. Samanlaisia laskuja suoritetaan bitti- ja merkkijonoille esimerkiksi silloin, kun joudutaan miettimään kaikkien mahdollisten salasanojen määrää ohjelmassa.
2. Majavaraiteet
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 6. Tehtävä oli tasoltaan helppo.
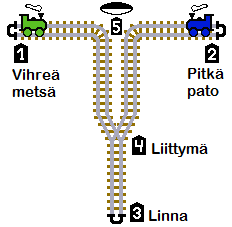 Majavien rautatiejärjestelmällä kulkee jatkuvasti kaksi junaa, vasemmalla vihreä ja oikealla sininen. Junat kulkevat seuraavien asemien välejä:
Majavien rautatiejärjestelmällä kulkee jatkuvasti kaksi junaa, vasemmalla vihreä ja oikealla sininen. Junat kulkevat seuraavien asemien välejä:
Vihreä välillä "Vihreä metsä" (1) ja "Linna" (3)
Sininen välillä "Pitkä pato" (2) ja "Linna" (3)
Yhdessä kohdassa (5) on kivi, jolla kontrolloidaan kumpaakin junaa. Kivessä on kaksi puolta, toinen on valkoinen ja toinen on musta. Kummankin junan kuljettajat voivat kääntää kiveä pysähtymällä kyseisessä kohdassa (5).
Rautatielle on asetettu kaksi liikennesääntöä. Ensimmäinen on:
SÄÄNTÖ "Linnaan"
- Jos kivi on musta, odota minuutti ja kokeile sääntöä "Linnaan" uudelleen.
- Jos kivi on valkoinen, käännä kivi mustaksi ja liiku kohtaan (3).
Mikä allaolevista on toinen SÄÄNTÖ "Linnasta", jonka avulla rautatie pysyy vapaana liikenneruuhkista ja joka estää junien yhteentörmäykset?
| 1. |
Vihreä juna ottaa suunnaksi "Vihreä metsä" (1) ja kääntää kiven valkoiseksi. |
Oikea vastaus |
| 2. |
Vihreä juna ottaa suunnaksi "Vihreä metsä" (1) ja kääntää kiven mustaksi. |
|
| 3. |
Vihreä juna ottaa suunnaksi "Pitkä pato" (2) ja kääntää kiven valkoiseksi. |
|
| 4. |
Vihreä juna ottaa suunnaksi "Vihreä metsä" (1) ja kääntää kiven mustaksi. |
Et vastannut tähän kysymykseen.
Selitys:
Oikeassa vastauksessa kummatkin junat suuntaavat kotiasemilleen (vihreä "Vihreään metsään" ja sininen "Pitkään patoon") ja kääntävät kiven valkoiseksi. Koska kumpikin juna linnaan mennessään kääntää kiven mustaksi, tietää toinen juna odottaa kunnes linnaan mennyt juna tulee takaisin ja kääntää kiven jälleen valkoiseksi. Näin junat tietävät milloin linnassa on toinen juna (musta kivi) ja milloin ei (valkoinen kivi) ja liikenneruuhkilta vältytään.
Tietojenkäsittelytieteissä usein eri tekijät käyttävät samoja resursseja, jotka voivat olla esimerkiksi aineistoja tai varastoja. Tällöin täytyy suunitella tarkoin miten samanaikainen käyttö onnistuu ilman vahinkoja tai sitä, että toinen tukkii toisen pääsyn resurssiin.
3. Tulitikut
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 6. Tehtävä oli tasoltaan helppo.
Tulitikut ovat ihanteellisia työkaluja numeroiden esittämiseen. Kuvassa on yleinen tapa esittää kymmenjärjestelmän numerot tulitikuilla. Tietyllä määrällä tulitikkuja voi muodostaa monia eri lukuja.
Mikä on pienin luku, jonka voi muodostaa 13 tulitikulla ilman nollia luvun alussa?
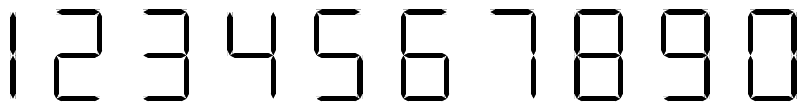
| 1. |
99 |
|
| 2. |
58 |
|
| 3. |
39 |
|
| 4. |
68 |
Oikea vastaus |
Et vastannut tähän kysymykseen.
Selitys:
Yhdessä numerossa voi käyttää enintään seitsemää tikkua. Jotta lukuun voisi käyttää tasan 13 tikkua, on luvun toisessa numerossa oltava siksi seitsemän ja toisessa kuusi tikkua. Vain numerossa kahdeksan voi käyttää seitsemää tikkua, joten luvun toisen numeron on oltava kahdeksan. Kuutta tikkua voi käyttää numeroissa 6, 9 ja 0. Tasan 13 tikulla voi siis muodostaa luvut 86, 89, 80, 68 ja 98, kun nollaa ei saa käyttää luvun alussa. Pienin näistä luvuista on 68.
Tehtävässä vaaditaan matemaattista laskukykyä sekä tietojenkäsittelytieteisiin liittyvää algoritmista ajattelua.
4. Majavakaupungin kadut
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 12. Tehtävä oli tasoltaan vaikea.
Alla on kaavio Majavakaupungin kaduista (kadut on merkitty kaavioon valkoisella). Kaikkia katuja on tarkkailtava valvontalaitteilla. Laitteita on neljää eri tyyppiä ja kaikilla näillä on eri hinnat.
Jokainen laite voi tarkkailla yhtä, kahta, kolmea tai neljää suuntaa koko kadun suoralta osalta. Laitteiden hinnat vaihtelevat tarkkailtavien suuntien määrän mukaan.
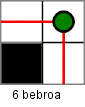
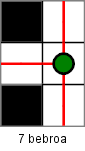
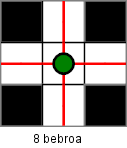
Kuinka paljon kaupungin kaikkien katujen tarkkailu vähintään maksaa?

| 1. |
31 |
Oikea vastaus |
| 2. |
33 |
|
| 3. |
34 |
|
| 4. |
32 |
Et vastannut tähän kysymykseen.
Selitys:
Voimme rakentaa kaksiosaisen graafin, jossa yksi kärkipisteiden joukko vastaa pystysuoria katuja ja toinen joukko vaakasuoria katuja. Kaaret niiden välillä kuvaavat katujen risteyksiin asetettuja kameroita. Kaaret painotetaan niiden niitä vastaavien kameroiden hinnoilla (6, 7 tai 8) ja jokainen käyttämätön kärkipiste saa arvon viisi.
Tehtävänä on nyt käyttää kaikkia kärkipisteitä mahdollisimman halvalla. Ensin etsimme sattumanvaraisen järjestyksen ja sitten parannamme sitä asteittain.
Tehtävän vois ratkaista myös kokeilemalla kuvaan eri vaihtoehtoja, kunnes ei enää löydy aiempia parempaa vaihtoehtoa.
Tehtävässä käsiteltiin optimoinnin ongelmaa, eli sitä, miten tavoite saavutetaan käyttämällä mahdollisimman vähän resursseja. Lisäksi tässä tutustuttiin. Ford-Fulkerson algoritmiin.

5. Eulerin polku
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 9. Tehtävä oli tasoltaan keskitaso.
Pikkumajava haluaa kiinnittää köyden muutaman puun väliin. Isämajava lupaa ostaa hänelle todella ison jäätelön, jos hän onnistuu kiinnittämään köyden puihin siten, että se kulkee vain kerran kunkin puuparin välillä.
Alla on esimerkki siitä, miten tämä esimerkiksi voitaisiin tehdä.
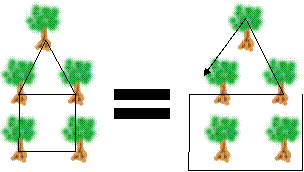
Mitä kuviota pikkumajava ei voi muodostaa isämajavan ohjeiden mukaan?
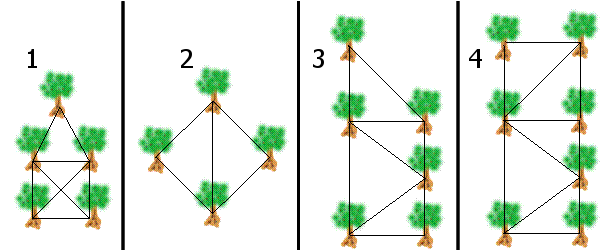
| 1. |
Kuvio 4 |
Oikea vastaus |
| 2. |
Kuvio 3 |
|
| 3. |
Kuvio 1 |
|
| 4. |
Kuvio 2 |
Et vastannut tähän kysymykseen.
Selitys:
Puulla, joka ei ole köyden alku- eikä loppupiste, on oltava parillinen määrä köyden osia. Siksi puun, jolla on pariton määrä köyden osia, täytyy olla köyden päässä.
Köydellä on tasan kaksi päätä ja siten kuviossa voi olla korkeintaan kaksi puuta, joilla on pariton määrä köyden osia.
- Vaihtoehdossa 1 puiden köyden osien määrät ovat 2, 3, 3, 4 ja 4. Se on mahdollista.
- Vaihtoehdossa 2 määrät ovat 2, 2, 3 ja 3. Se on oikein.
- Vaihtoehdossa 3 määrät ovat 2, 2, 3, 3, 4 ja 4. Se on myös oikein.
- Vaihtoehdossa 4 nämä määrät ovat 2, 2, 3, 3, 4, 4 ja 5. Se tekee Eulerin polusta mahdottoman.
Tietojenkäsittelytieteessä usein joudutaan etsimään ratkaisua jonkin annetun ehdon perusteella. Ratkaisun etsiminen annetuilla alkuehdoilla on aina algoritminen tehtävä. Tässä tehtävässä ehtona on etsiä ratkaisu siten, että muodostuu Eulerin polku (http://fi.wikipedia.org/wiki/Eulerin_polku).
6. Listan muunnoksia
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 12. Tehtävä oli tasoltaan vaikea.
Seuraavaa rakennetta voidaan käyttää määriteltäessä uusia numerolistoja lausekkeen ja numerolistan avulla
[lauseke FOR x IN list] .
Rakenteessa olevan lausekkeen on oltava muuttujan x sisältävä matemaattinen lauseke. Jokainen numerolistan jäsen sijoitetaan lausekkeeseen muuttujan x paikalle ja siten saadaan uusi numerolista.
Esimerkiksi rakenne [x + 1 FOR x IN 1,2,3,4,5] tuottaa listan "2,3,4,5,6".
Mikä seuraavista lausekkeista voidaan sijoittaa alla olevaan rakenteeseen kolmen pisteen tilalle niin, että rakenne määrittelee vähenevän listan?
[x2 FOR x IN [... FOR x IN 1, 2, 3, 4]]
| 1. |
x - 10 |
Oikea vastaus |
| 2. |
x - 2 |
|
| 3. |
2x + 1 |
|
| 4. |
x + 5 |
Et vastannut tähän kysymykseen.
Selitys:
Annetuilla lausekkeilla listat muuttuvat seuraavasti:
A: [1, 2, 3, 4] > [3, 5, 7, 9] > [9, 25, 49, 81] (kasvava lista)
B: [1, 2, 3, 4] > [-1, 0, 1, 2] > [1, 0, 1, 4] (ensin vähenevä, sitten kasvava lista)
C: [1, 2, 3, 4] > [6, 7, 8, 9] > [36, 49, 64, 81] (kasvava lista)
D: [1, 2, 3, 4] > [-9, -8, -7, -6] > [81, 64, 49, 36] (vähenevä lista)
7. Loogiset toiminnot - kirjain E
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 12. Tehtävä oli tasoltaan vaikea.
Tietokonegrafiikassakin voidaan käyttää loogisia toimintoja. Kahden toisiaan leikkaavan alueen leikkaus tarkoittaa aluetta, jolla alueet ovat päällekkäin. Kahden alueen yhdiste tarkoittaa aluetta, joka muodostuu yhdistämällä alueet. Kahden toisiaan leikkaavan alueen X ja Y erotus erotus (X, Y) tarkoittaa sitä aluetta, jolla on pelkästään X.
Käytössä on toiminnot leikkaus (X, Y), yhdiste (X, Y) ja erotus (X, Y).
Ilmaisu yhdiste (leikkaus (X, Y), Z) tarkoittaa alueiden X ja Y leikkauksen yhdistettä alueen Z kanssa.
Mitä loogisia toimintoja käyttäen saadaan muodostettua kirjain e kahdesta ellipsistä A ja B sekä kahdesta suorakulmiosta C ja D?

| 1. |
Kirjainta "e" ei voi muodostaa näillä toiminnoilla näistä kappaleista. |
|
| 2. |
erotus (leikkaus (erotus (A, B), C), D) |
|
| 3. |
erotus (yhdiste (erotus (A, B), C), D) |
Oikea vastaus |
| 4. |
leikkaus (A, erotus (B, yhdiste(C, D))) |
Et vastannut tähän kysymykseen.
Selitys:
Voimme muodostaa kirjaimen e kolmella askeleella (katso kuva).
1) poistetaan pieni ellipsi suuresta: erotus (A, B)
2) lisätään edelliseen yksi suorakulmio: yhdiste (erotus (A, B), C)
3) poistetaan toinen suorakulmio edellisestä: erotus (yhdiste (erotus (A, B), C), D)
Vastaukset 2 ja 3 johtavat erilaisiin lopputuloksiin.
Tietojenkäsittelyssä ne säännöt miten objekti luodaan ovat usein tärkeämpiä ymmärtää kuin itse objekti. Nämä matematiikastakin tutut toiminnot ovat osa jokaista graafista vektorigrafiikkaohjelmaa. Yksinkertaisilla toiminnoilla voidaan luoda monimutkaisia ja suuriakin kuvia.

8. Laula laulu
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 9. Tehtävä oli tasoltaan keskitaso.
Pupu Banaani on uusin teinipopin tähti Majavamaassa. Kaikki nuoret majavat haluavat laulaa kuten hän. Hän selittää laulunsa seuraavasti.
- Lause koostuu lyhyistä sanoista, jotka on luotu yhdestä konsonantista ('b', 'd', 'p', ...) ja yhdestä vokaalista ('a', 'e', 'i', ...), kuten 'da', 'nu', 'si', ...
- Säe on samojen lyhyiden sanojen sarja (sanoja pariton määrä), jossa keskimmäiseen sanaan on lisätty 'p di', kuten 'da dap di da' tai 'ne ne nep di ne ne', ...
- Laulu koostuu yhdestä tai useammasta säkeestä ja jos se koostuu useammasta kuin yhdestä säkeestä, se voidaan lopettaa sanalla 'jee'.
Neljä majavaa yrittää matkia Pupua, mutta vain yksi onnistuu. Kuka?
| 1. |
Maisa, joka laulaa: sa sa sap di sa sa lu lu lup di lu lu jee. |
Oikea vastaus |
| 2. |
Mira, joka laulaa: da da dap di da da jee. |
|
| 3. |
Mikko, joka laulaa: nu nu nup di nu nu di di dip di di. |
|
| 4. |
Marko, joka laulaa: si sip di si su dup di su. |
Et vastannut tähän kysymykseen.
Selitys:
- Marko laulaa väärin; laulussa täytyisi olla dup:in tilalla sup.
- Mira laulaa väärin; 'jee' ei voi esiintyä vain yhden säkeen jälkeen.
- Mikko laulaa väärin; lopusta puuttuu yksi 'di'.
Pupu Banaanin kieli kuvaa 'formaalin kielen' rakennetta, eli se on kuin kielioppia. Tietojenkäsittelytieteissä kielioppia käytetään kuvaamaan myös ohjelmointikielien rakennetta.
9. Sateenkaaren värit
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 6. Tehtävä oli tasoltaan helppo.
Liina värjää kananmunia. Hän käyttää kolmea värikuppia. Keltaista ja punaista väriä on paljon, joten hän voi kastaa kaksi kolmasosaa kustakin kananmunasta keltaiseen tai punaiseen väriin. Sinistä väriä on vähän, joten hän voi kastaa ainoastaan kolmasosan kustakin kananmunasta siniseen väriin. Liina kastaa jokaisen kananmunan niin syvälle kuin mahdollista.
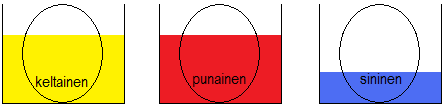
Värit muuttuvat sekoittuessaan seuraavasti:
- Keltainen ja punainen muodostavat oranssin.
- Keltainen ja sininen muodostavat vihreän.
- Punainen ja sininen muodostavat violetin.
Liina ei ikinä sekoita useampaa kuin kahta väriä.
Esimerkiksi: Liina kastaa yhden kananmunan punaiseen väriin, sen jälkeen siniseen ja sen jälkeen hän kääntää kananmunan ympäri ja kastaa sen siniseen. Näin hän saa kananmunan, joka on väriltään violetti-punainen-sininen.
Mikä seuraavista kananmunista on Liinan kastama?
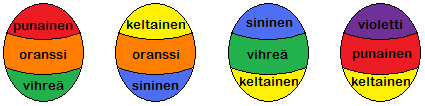
| 1. |
Sininen-vihreä-keltainen |
|
| 2. |
Punainen-oranssi-vihreä |
Oikea vastaus |
| 3. |
Violetti-punainen-keltainen |
|
| 4. |
Keltainen-oranssi-sininen |
Et vastannut tähän kysymykseen.
Selitys:
Liina värjää kananmunan seuraavasti:
Ensin hän kastaa kananmunan punaiseen (valkoinen-punainen-punainen), hän kääntää munan (punainen-punainen-valkoinen), kastaa sen keltaiseen (punainen-oranssi-keltainen) ja lopuksi kastaa sen siniseen (punainen-oranssi-vihreä).
Keltainen-oranssi-sininen muna on mahdoton, koska keskellä oranssi tarvitsee punaista, mutta kärkien keltainen ja sininen ovat päävärejä.
Sininen-vihreä-keltainen muna on mahdoton, koska keskellä vihreä tarvitsee sinistä, mutta sininen väri ei yllä kärkeä pitemmälle.
Violetti-punainen-keltainen muna on mahdoton, koska Leena upottaa munat mahdollisimman syvälle, joten jos yksi kärki on keltainen, täytyy keskikohdankin olla keltainen tai oranssi.
Kysymys siitä, kuuluuko annettu muna Leenan mahdollisten munien joukkoon, on päätösongelma. Jotta päätöksen voisi tehdä automaattisesti, Leenan munien joukkoa täytyy kuvata säännöllisellä kielellä, tässä esimerkissä värityssäännöillä. Ohjelmointikielillä on tietojenkäsittelyssä niin ikään formaalit kieliopit, jolloin on helppo tarkastaa noudattaako koodi kielioppia vai onko siellä virheitä.
10. Katkennut oksa
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 9. Tehtävä oli tasoltaan keskitaso.
Majavamutkan kylässä kasvaa erikoinen puu. Puun runko haarautuu kahteen pienempään haaraan ja kukin haara haarautuu aina kahteen uuteen. Puun jokaisen pienimmän oksan päässä on lehti. Joka vuosi pienimpien oksien kärjistä kasvaa kaksi uutta oksaa ja näiden uusien oksien kärkiin kasvaa yksi lehti kuhunkin. Täten puulla on yksi lehti kasvunsa ensimmäisenä vuonna, kaksi lehteä toisena ja niin edelleen.
Kerran tällaisen puun pienin oksa katkesi eikä se oksa kasvanut enää sen jälkeen. Puusta voidaan kuitenkin selvittää puun todellinen ikä ja jopa se, milloin oksa on katkennut, laskemalla puusta pudonneet lehdet. Esimerkiksi, jos oksa on katkennut kolmantena vuonna ja puu olisi nyt viisivuotias, siinä olisi kaksitoista lehteä kuudentoista sijaan.
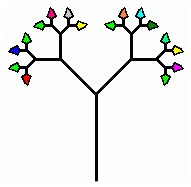
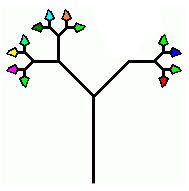
Mitä määrää lehtiä puussa ei voi olla, jos siitä on katkennut vain yksi oksa?
| 1. |
18 |
Oikea vastaus |
| 2. |
24 |
|
| 3. |
14 |
|
| 4. |
30 |
Et vastannut tähän kysymykseen.
Selitys:
Jos yksikään oksa ei katkea, lehtien määrä kaksinkertaistuu joka vuosi: 1, 2, 4, 8, 16, 32, 64…
Jos oksa katkeaa ensimmäisenä vuonna: 1, 1, 2, 4, 8, 16, 32…
Toisena vuonna: 1, 2, 3, 6, 12, 24, 48…
Kolmantena vuonna: 1, 2, 4, 7, 14, 28, 56...
Neljäntenä vuonna: 1, 2, 4, 8, 15, 30, 60...
Viidentenä vuonna: 1, 2, 4, 8, 16, 31, 62...
Itse asiassa lehtien lukumäärä on aina kahden 2:n potenssin erotus.
Koskaan ei puussa voisi siis olla 18 lehteä, kaikki muut vaihtoehdot ovat mahdollisia.
Tehtävä mallintaa eksponentiaalista kasvua (http://fi.wikipedia.org/wiki/Eksponentiaalinen_kasvu) luonnossa. Ongelman ratkaisemiseksi vaaditaan algoritmista ajattelua ja tehtävä sisältää myös kombinatorisen rakenteen.
11. Tasapainotila
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 9. Tehtävä oli tasoltaan keskitaso.
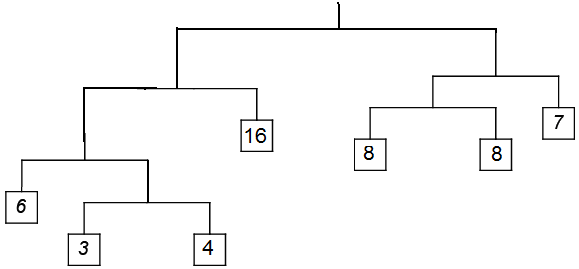
Kuvan mobile ei todellisuudessa ole tasapainossa. Ylimmältä tasolta tarkasteltuna vasemmalla puolella on painoa 29 ja oikealla puolella 23 yksikön verran (mobilen muut osat eivät vaikuta tasapainoon).
Mikä on pienin määrä painoja, joita täytyy muuttaa, jotta mobile ja jokainen mobilen sisältämä pienempi mobile olisi tasapainossa?
| 1. |
3 |
Oikea vastaus |
| 2. |
4 |
|
| 3. |
1 |
|
| 4. |
2 |
Et vastannut tähän kysymykseen.
Selitys:
Ratkaisun avain on, että alemmalla tasolla täytyy painon olla aina puolet ylemmän tason painosta. Mobilessa on valmiina neljä painoa (4, 8, 8 ja 16), jotka noudattavat tätä sääntöä. Mobilen koko painon on oltava tällöin 64 ja alemmilla tasoilla on oltava painoa 32, 16, 8 ja 4. Kolmea mobileen jäljelle jäänyttä painoa (3, 6 ja 7) muuttamalla mobile saadaan kaikilla tasoilla tasapainoon.
Tehtävässä vaaditaan loogista päättelykykyä, mikä on tärkeää monissa tietojenkäsittelytieteeseen liittyvissä asioissa.
12. Karel kävelee kuutiolla
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 12. Tehtävä oli tasoltaan vaikea.
 Karel on robotti. Hän liikkuu hänelle annettujen ohjeiden mukaan.
Karel on robotti. Hän liikkuu hänelle annettujen ohjeiden mukaan.
ASTU – hän liikkuu yhden askeleen eteenpäin seuraavalle tahkolle.
VASEN – hän kääntyy 90 astetta vasempaan.
Esimerkki 1: Jos Karelille on annettu ohjeet ASTU-ASTU-VASEN-ASTU, hän liikkuu kuin ratsu tavallisella shakkilaudalla.
Esimerkki 2: Jos Karel seisoo kuutiolla ja hänelle on annettu ohjeet ASTU-ASTU-ASTU-ASTU, hän palaa takaisin tahkolle, jolla hän oli aluksi.
Karel seisoo nyt kuutiolla. Hänen on käytävä kaikilla kuution tahkoilla, mutta kullakin vain kerran!
Huomaa, että OIKEA-komentoa Karel ei tunnista.
Mikä on pienin määrä komentoja, joilla Karel voi suorittaa tehtävän?
| 1. |
9 |
Oikea vastaus |
| 2. |
10 |
|
| 3. |
Näiden ohjeiden mukaan kuution kaikilla tahkoilla käyminen vain kerran ei ole mahdollista. |
|
| 4. |
7 |
Et vastannut tähän kysymykseen.
Selitys:
Kuution pinta voidaan purkaa vain 11 erilaiseen muotoon (matemaatikot sanovat “kuution verkot” – katso kuva). Näistä x:llä merkittyjä ei voida kävellä läpi ilman takaisin kääntymistä (niissä on ”risteyksiä”). Niihin joiden läpi Karel voi kävellä, on piirretty sininen viiva. Kuvista voi huomata, että jokainen tie sisältää ainakin yhden käännöksen vasempaan ja yhden oikeaan. Karelin on käytävä kuution jokaisella tahkolla, joten hänen on käytettävä ASTU-komentoa viisi kertaa. Hänen on myös käännyttävä kerran vasempaan ja kerran oikeaan. Koska oikealle kääntymiseen ei ole komentoa, hänen täytyy käyttää oikealle kääntymiseen kolme VASEN-komentoa. Karel tarvitsee ainakin neljä VASEN-komentoa ja viisi ASTU-komentoa, joten käskyjen pienin mahdollinen määrä on yhdeksän.
Tietojenkäsittelytieteisiin kuuluu algoritminen ajattelu, mitä esimerkiksi tehtävän robotin ohjelmointi on.

13. Sekoitettu väri
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 6. Tehtävä oli tasoltaan helppo.
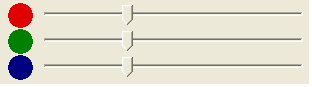
Kristian piirteli kuvankäsittelyohjelmalla. Hän loi värisävyn sekoittamalla kolmea perusväriä (punaista, vihreätä ja sinistä) asettaen saman arvon kullekin perusvärille.
Mitä värisävyä hän ei voi tällä tavoin saada?
| 1. |
Keltainen |
Oikea vastaus |
| 2. |
Valkoinen |
|
| 3. |
Harmaa |
|
| 4. |
Musta |
Et vastannut tähän kysymykseen.
Selitys:
Kaikki ruudulla näkyvät pikselit muodostuvat kolmesta värikomponentista: punaisesta, vihreästä ja sinisestä. Jokainen liukusäädin määrittää kustakin komponentista suodattuvan valon määrän.
Tummuus tarkoittaa valottomuutta, joten mustan värin saadakseen täytyy asettaa kaikki arvot nollaan. Valkoisella värillä on suurin mahdollinen kirkkaus, joten saadakseen sitä täytyy asettaa kaikki arvot maksimiin, joka on yleensä 255. Koska harmaan sävyt ovat näiden kahden värin välissä, harmaan värin arvot ovat yhden ja 254:n välissä.
Keltaista saadakseen täytyy yhdistää vain punaista ja vihreää väriä, ei yhtään sinistä. Täytyy siis asettaa punaiselle ja vihreälle arvo 255 ja siniselle arvo 0.

Kuvankäsittelytyökalujen tuntemus ja ymmärtäminen kuuluvat läheisesti tietojenkäsittelytieteisiin.
14. Menninkäiset
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 6. Tehtävä oli tasoltaan helppo.
Hyvät menninkäiset puhuvat aina totta, pahat menninkäiset valehtelevat aina. Valitettavasti et pysty erottaman heitä toisistaan.
Tapaat metsässä kolme menninkäistä. Heistä ensimmäinen kertoo sinulle, että kaksi muuta ovat pahoja. Toinen heistä kieltää olevansa paha. Kolmas väittää toisen menninkäisen olevan paha.
Kuinka monta pahaa menninkäistä olet tavannut?
| 1. |
2 |
Oikea vastaus |
| 2. |
3 |
|
| 3. |
0 |
|
| 4. |
1 |
Et vastannut tähän kysymykseen.
Selitys:
Jos kolmas on paha, niin toinen on hyvä. Jos kolmas on hyvä, niin toinen on paha. Molemmissa tapauksissa ensimmäinen valehteli. Kohtasit siis kaksi pahaa menninkäistä.
Tehtävä vaatii eri tapausten erottamista toisistaan ja niiden analysoimista loogisia operaatioita käyttäen. Näin voidaan tietojenkäsittelytieteen keinoin päästä oikeaan ratkaisuun.
15. Sukupuu
Sait 0 pistettä tästä tehtävästä. Tehtävän maksimipistemäärä on 12. Tehtävä oli tasoltaan vaikea.
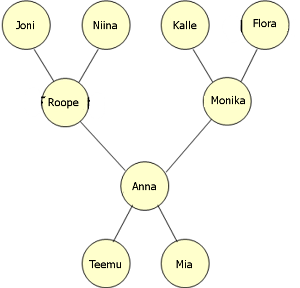
Tämä sukupuu kuvaa erään majavasuvun jäseniä. Ylimpänä ovat suvun vanhimmat ja alimpana nuorimmat jäsenet.
Tässä tapauksessa Monika on Teemun ja Mian isoäiti.
Haluamme kirjoittaa tietokoneelle ohjelman, joka voi määrittää onko joku tietyn henkilön esivanhempi.
Lapsi määritettäisiin näin:
A onLapsiHenkilölle B.
Lapsenlapsi taas voitaisiin määrittää seuraavalla tavalla:
A onLapsenlapsiHenkilölle C = (A onLapsiHenkilölle B ja B onLapsiHenkilölle C).
Kuinka määrittäisit esivanhemman, joka tässä tapauksessa voisi olla vanhempi tai kuka tahansa muu ylenevässä polvessa?
| 1. |
A onEsivanhempiHenkilölle C = (A onEsivanhempiHenkilölle B ja B onEsivanhempiHenkilölle C) |
|
| 2. |
A onEsivanhempiHenkilölle C = (A onEsivanhempiHenkilölle B ja B onVanhempiHenkilölle C) |
|
| 3. |
A onEsivanhempiHenkilölle C = (A onVanhempiHenkilölle C tai (B onVanhempiHenkilölle C ja A onEsivanhempiHenkilölle B)) |
Oikea vastaus |
| 4. |
A onEsivanhempiHenkilölle C = (A onVanhempiHenkilölle B ja B onVanhempiHenkilölle C) |
Et vastannut tähän kysymykseen.
Selitys:
Esivanhempi voi olla vanhempi tai kuka tahansa vanhemman esi-isä. Ensimmäinen vastaus määrittää isovanhemmat, toinen on ääretön itseäänkutsuva määritelmä. Viimeisessä vastauksessa vanhemmat puuttuvat esivanhempien joukosta.
Tehtävässä pitää seurata käskyjä ja siinä saa ajatuksen binääripuusta (http://fi.wikipedia.org/wiki/Bin%C3%A4%C3%A4ripuu), mikä on tietojenkäsittelytieteessä käytetty tietorakenne.




